Cảm ơn các bạn đã ghé thăm blog. Bài viết này tổng hợp các công thức đạo hàm logarit và mũ giúp các bạn tra cứu nhanh nhất.
CÔNG THỨC TÍNH ĐẠO HÀM LOGARIT
Cho hàm số 
. Khi đó đạo hàm của hàm số trên là:
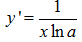
Trường hợp tổng quát hơn, cho hàm số 
. Đạo hàm là:
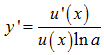
Ví dụ:
Tính đạo hàm của hàm số 
.
Lời giải:
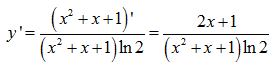Trường hợp đặc biệt, khi cơ số của hàm logarit là e. Hay y=lnx. Ta có công thức đạo hàm như sau:
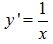Nếu y=lnu(x) thì ta có:
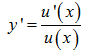
CÔNG THỨC TÍNH ĐẠO HÀM MŨ
Cho hàm số 
. Đạo hàm của hàm số là:
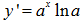Trường hợp tổng quát hơn, 
. Ta có:
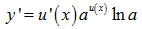
Ví dụ:
Tính đạo hàm của hàm số 
.
Lời giải:
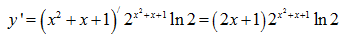
Đặc biệt, nếu cơ số của hàm mũ là e. Hay 
. ta có công thức:
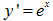Ta thấy đây là hàm số mà ta đạo hàm bao nhiêu lần thì hàm số cũng không thay đổi.
Nếu 
thì ta có công thức:
Trên đây là toàn bộ công thức tính đạo hàm logarit và mũ. Để tiện lợi cho các bạn lưu lại để học tôi sẽ tổng hợp lại trong bảng công thức tính đạo hàm logarit mũ sau đây:
Trong các công thức trên thì công thức số 4 và số 8 là 2 công thức tổng quát. Các bạn nhớ 2 công thức này là có thể tự suy ra các công thức còn lại. Chẳng hạn chúng ta chỉ cần lưu ý (x)’=1. Khi đó các bạn thay u=x vào các công thức 4 và 8 là ta thu được công thức 3 và 7. Hay khi các bạn thay a=e, thay u=x thì các bạn được công thức 1 và 5. Khi các bạn thay a=e thì ta được công thức 2 và 6. Thật đơn giản phải không nào! Chúc các bạn học tập vui vẻ!