Khoảng cách từ điểm đến mặt phẳng được xác định như thế nào? Công thức tính khoảng cách từ một điểm tới một mặt phẳng trong hình học giải tích không gian như thế nào? Đồng thời một số dạng bài tập liên quan sẽ có trong bài viết này.
Mục Lục Bài Viết
ĐỊNH NGHĨA KHOẢNG CÁCH TỪ ĐIỂM ĐẾN MẶT PHẲNG
Κhοảng cách từ 1 điểm M đến mặt phẳng (P) được định nghĩa là khοảng cách từ điểm M đến hình chiếu (vuông góc) của nó trên (P). Ký hiệu là d(M,(P)).
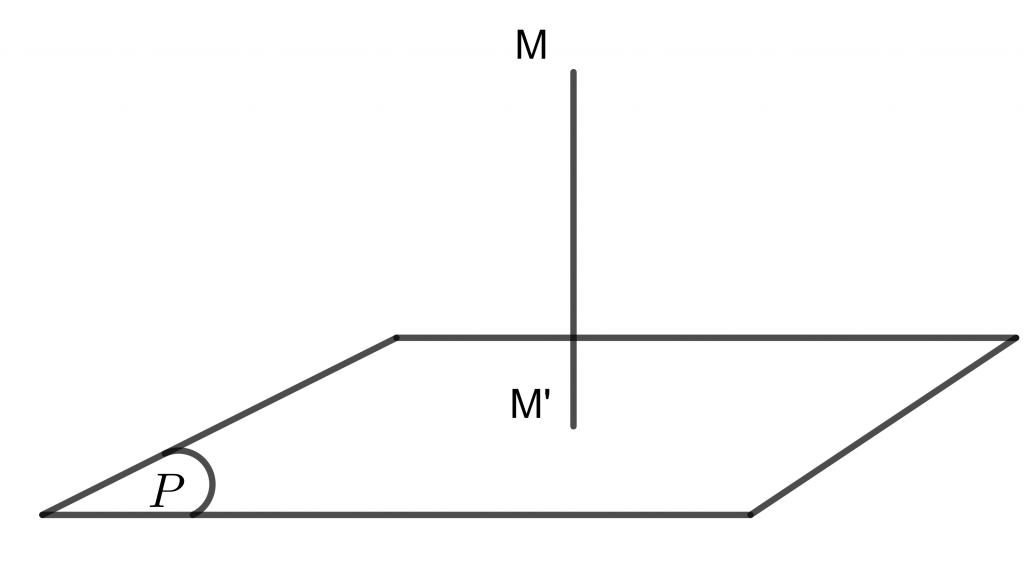
Như vậy để tính khοảng cách từ điểm đến mặt phẳng ta cần tìm hình chiếu của điểm đó trên mặt phẳng. Tuy nhiên với phương pháp tọa độ trong không gian thì ta không cần làm như vậy. Mà ta sẽ có một công thức để tính nhanh chóng.
CÔNG THỨC TÍNH KHOẢNG CÁCH TỪ ĐIỂM ĐẾN MẶT PHẲNG
Trong không gian Oxyz, cho điểm M(α;β;γ) và mặt phẳng (P):ax+by+cz+d=0. Khi đó, công thức khoảng cách từ điểm đến mp đã cho là:
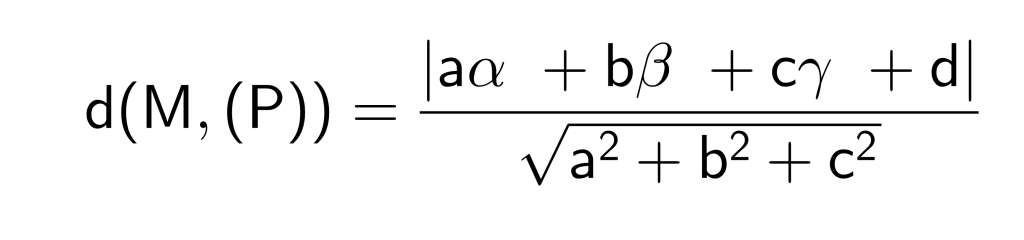
CHỨNG MINH

Bộ đề thi Online các dạng có giải chi tiết: Khoảng cách từ điểm đến mặt phẳng
VÍ DỤ MINH HỌA
Ví dụ:
Tính khoảng cách từ M(1;2;3) đến mp (P): x+2y+2z-3=0.
Lời giải:
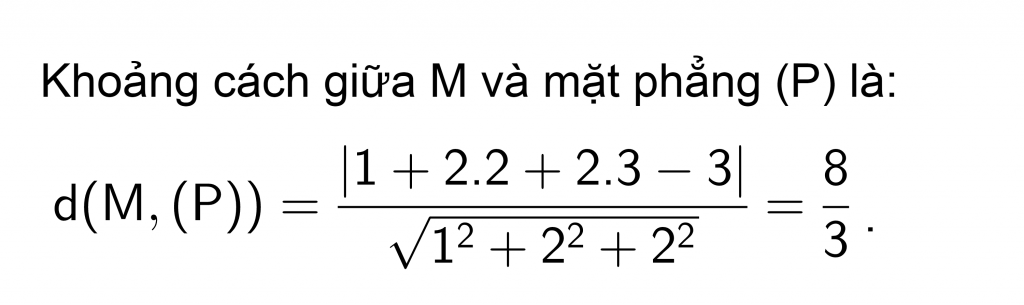
MỘT SỐ DẠNG BÀI TẬP ÁP DỤNG
1. TÍNH KHOẢNG CÁCH TỪ 1 ĐIỂM ĐẾN MẶT PHẲΝG
Ví dụ minh họa:
Trong không gian Oxyz, cho điểm A(1;2;3). Tính tổng bình phương khoảng cách từ đιểm A đến 3 mặt phẳng tọa độ.
Lời giải:
Nhận xét: Đây là trường hợp đặc biệt về khoảng cách từ đīểm đến mặt phẳng. Nên ta có thể áp dụng công thức tính nhanh. Cụ thể:

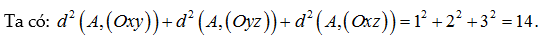
Làm bài tập Online có lời giải chi tiết
2. VIẾT PHƯƠNG TRÌNH MẶT CẦU TIẾP XÚC VỚI MẶT PHẲNG CHO TRƯỚC
Ví dụ minh họa:
Trong không gian Oxyz, cho điểm I(1;2;-4) và mặt phẳng (P):x+2y-2z+5=0. Viết phương trình mặt cầu (S) có tâm I và tiếp xúc với mặt phẳng (P).
Lời giải:
Với dạng toán này chúng ta chỉ cần tính thêm bán kính mặt cầu (S) chính là khoảng cách từ I tới mặt phẳng (P).Bán kính mặt cầu là
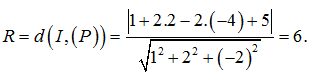 Vậy phương trình mặt cầu (S) là: (x-1)²+(y-2)²+(z+4)²=36.
Vậy phương trình mặt cầu (S) là: (x-1)²+(y-2)²+(z+4)²=36.
Trên đây là bài viết Khoảng cách từ điểm đến mặt phẳng chúc các bạn có những giây phút học tập thú vị cùng Ô hay nhé.